Messed up BMA maps

[OntarioHunter]

I don't have On-X because I mostly hunt birds on BMA, WMA, and federal refuges with well defined borders. But I will be hunting deer in a few days so I opened up the BMA maps to do a little scouting. While the BMA units are clearly defined, BLM land is clearly unclear. They chose light yellow that is so light it is pretty much undiscernable from private land white. I don't recall having this trouble in years past. Perhaps FWP is trying to step BLM color a bit further away from Indian reservation tan color? Anyone else notice this? I do have a Montana Land Use Atlas so can cross reference with it. However, besides being quite out of date, the Atlas is not 100% accurate for determining land ownership. I use it mostly for better geography detail.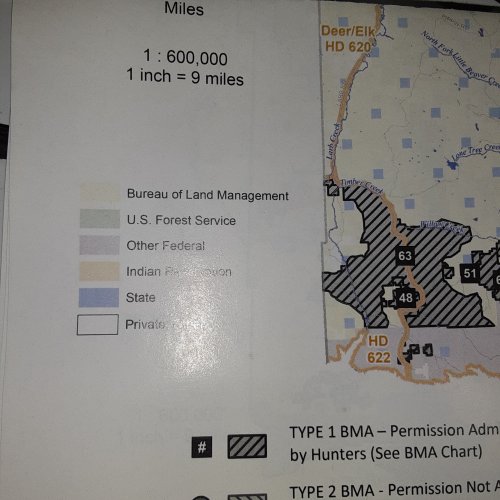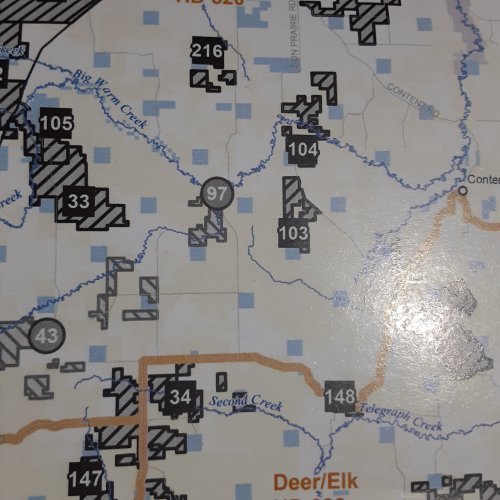The land in this section is a checkerboard of BLM and private land. Can you differentiate the boundaries?

 

[BuckRut]

I don't think that maps intended use is that detailed. Boundaries on those maps are anything but clearly defined. Yes they have nice dark lines but you have to get the area specific map for any kind of details. Tall task to expect the FWP to put that much detail into a map only intended to convey the general area and BMA numbers.

 

[Irrelevant]

1. try turning to one of the bma maps for more detail.
2. get onx.

 

[brocksw]

Where's the "you are here"? That would help tremendously.

 

[mtmiller]

https://fwp.mt.gov/binaries/content/assets/fwp/gisresources/hunting/hunteraccess/blockman/region6maps2022.pdf

Or stop in the Malta BLM office and pick up some 1:100k maps. $4 a pop or just break down and spend $25 for OnX.

 

[mtmiller]

This should be right up your alley.

The app is pretty intuitive! Once you click the icon to start a route, you can put your phone down and drive, and when you arrive, hit the end route icon, and then you can go back via the website and enter observations, if you had any from that trip. Even if you didn't have any observations, that's OK - the data is still useful. A route can be a short or long drive. We're trying to outreach to folks who drive between towns and cities on the Hi-Line on a regular basis, from Shelby to Glasgow. The best way to input individual observations is as a passenger. Website: www.wildlifexing.org

 

[OntarioHunter]

https://fwp.mt.gov/binaries/content/assets/fwp/gisresources/hunting/hunteraccess/blockman/region6maps2022.pdf

Or stop in the Malta BLM office and pick up some 1:100k maps. $4 a pop or just break down and spend $25 for OnX.

Doesn't OnX require cell coverage? I'm out of range quite a bit of the time deer hunting. I've also heard using it saps the phone's battery. Do USGS 1:100 maps differentiate property ownership?

I'm more interested in public land that is NOT BMA.

 

[AvidIndoorsman]

Doesn't OnX require cell coverage?

It does not. You download the area you are hunting and then it works offline.

 

[Deleted member 20812]

Do USGS 1:100 maps differentiate property ownership?

The BLM maps show private and public land but do not differentiate private land at all.

 

[OntarioHunter]

The BLM maps show private and public land but do not differentiate private land at all.

So you're saying there's no color differentiation showing what is public and what is private land?

 

[MNElkNut]

Just get OnX. The rest of us are avid hunters. We have OnX and recommend it for a reason. We are not getting paid to say that! No cell coverage necessary after you download the area you will be in. You will use it a LOT.

 

[Gerald Martin]

Get OnX. You will wonder why you ever waited so long.

 

[Deleted member 20812]

So you're saying there's no color differentiation showing what is public and what is private land?

No. I’m saying there is color differentiation between public and private, to include different agency ownership. There is no differentiation between private parcels as far as ownership.

I agree with the others. For $25 it’s stupid not to buy OnX.

 

[brocksw]

....stupid not to buy OnX.

^^^^^^^^^^^^^^^^^^^^

 

[Deleted member 20812]

Or Basemap (I think?).

At $4 per map, you get three of them and you’re at half a subscription.

 

[Walkathon]

I second Onx. Works great and you can download the map area you want and use in airplane mode. I used in MT a couple of weeks ago in areas with no service. Worked great.

 

[Bambistew]

The cartographers at F&G...

 

[AvidIndoorsman]

The cartographers at F&G...

Teaching boomers to open .pdfs and gritting your teeth and using Arial are actually contractual obligations.

 

[Hem]

Teaching boomers to open .pdfs and gritting your teeth and using Arial are actually contractual obligations.

I resent that comment punk.
Though partially true.

 

[MTTW]

I've also heard using it saps the phone's battery.

onx runs my phone's battery dead so fast that I am going back to paper topo maps and use the compass on inreach. I will admit to being totally frustrated with electronic shit, and I am surely doing something wrong on my end. It is great for locating property lines though, which I rarely do. I also have an old gps that was given to me that I can partially run.

Electronically frustrated boomer, formerly known as Chad